
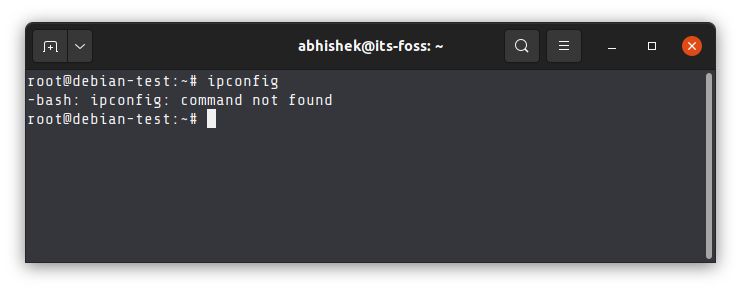
When you use commands in Linux, you expect to see an output. But sometimes, you’ll encounter issues where the terminal shows ‘command not found’ error.
There is no straightforward, single solution to this error. You have to do a little bit of troubleshooting on your own.
It’s not too difficult, honestly. The error gives some hint already when it says “bash: command not found”. Your shell (or Linux system) cannot find the command you entered.
There could be three possible reasons why it cannot find the command:
- It’s a typo and the command name is misspelled
- The command is not even installed
- The command is basically an executable script and its location is not known
Let’s go in detail on each possible root cause.
Fixing “bash: command not found” error

Method 1: Double check the command name (no, seriously)
It is human to make mistakes, specially while typing. It is possible that the command you entered has a typo (spelling mistake).
You should specially pay attention to:
- The correct command name
- The spaces between the command and its options
- The use of 1 (numeral one), I (capital i) and l (lowercase L)
- Use of uppercase and lowercase characters
Take a look at the example below, where I have misspelled the common ls command.
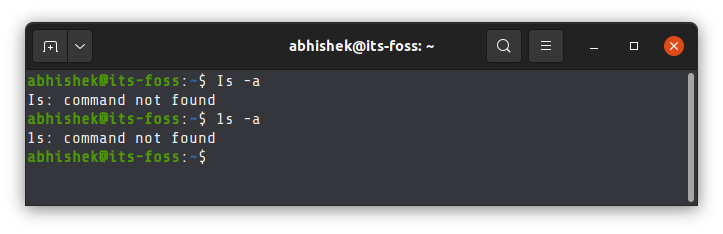
So, make double sure what you are typing.
Method 2: Ensure that the command is installed on your system
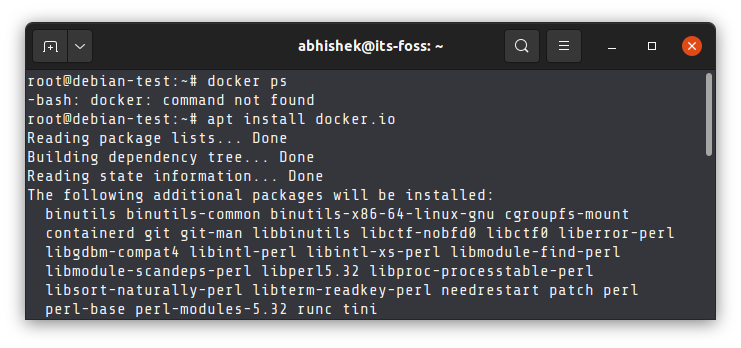
This is another common reason behind the command not found error. You cannot run a command if it is not installed already.
While your Linux distribution comes with a huge number of commands installed by default, it is not possible to pre-install all the command line tools in a system. If the command you are trying to run is not a popular, common command, you’ll have to install it first.
You can use your distribution’s package manager to install it.
In some cases, popular commands may get discontinued and you may not even install it anymore. You’ll have to find an alternative command to achieve the result.
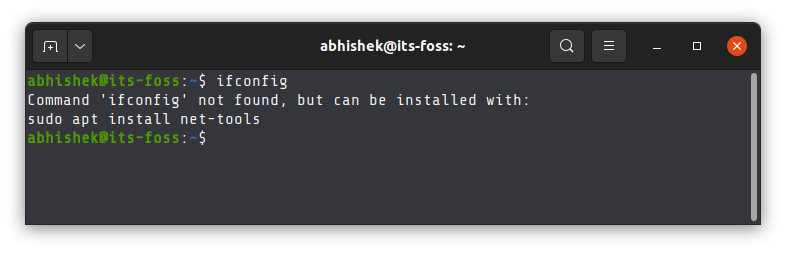
Take the example of ifconfig command. This deprecated command was used for getting Ip address and other network interface information. Older tutorials on the web still mention using this command but you cannot use it anymore in newer Linux versions. It has been replaced by the ip tool.
Occasionally, your system won’t find even the extremely common commands. This is often the case when you are running a Linux distribution in Docker containers. To cut down on the size of the operating system image, the containers often do not include even the most common Linux commands.
This is why Docker user stumble across things like ping command not found error etc.
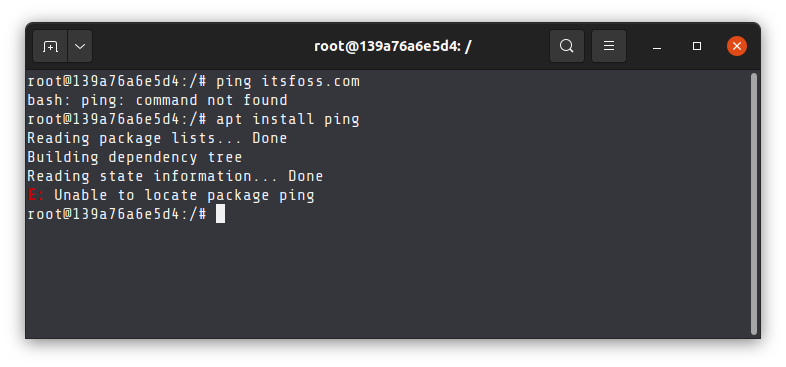
So, the solution is to either install the missing command or find a tool that could do the same thing you were trying to do with the missing command.
Method 3: Make sure that the command is real, not an alias
I hope you are aware of the alias concept in Linux. You can configure your own shorter commands to replace the typing of a longer command.
Some distributions like Ubuntu automatically provide commands like ll (which is aliased to ls -l), la (aliased to ls -a) and so on.
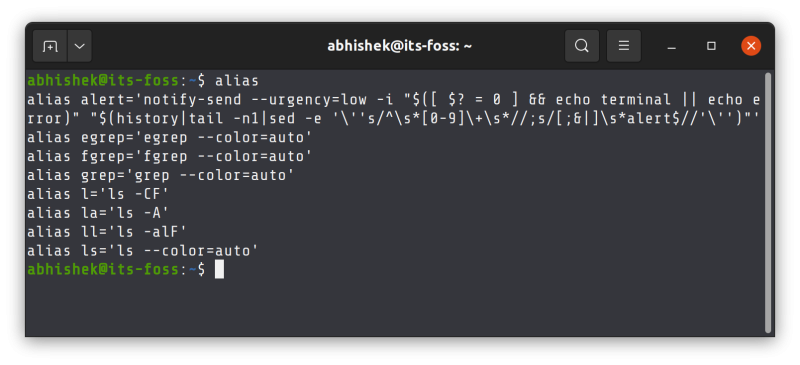
Imagine that you are used to of typing ll and la on your personal system and you log on to another Linux system and find that ll command does not exist. You cannot even install the ll command because it is not a real command.
So, if you cannot find a command and it cannot even be installed, you should try searching on the internet if that command even exists. If it does not, probably it was an alias on some other system.
Method 4: Check if it is an executable script with correct path
This is a common mistake Linux rookies make while running a shell script.
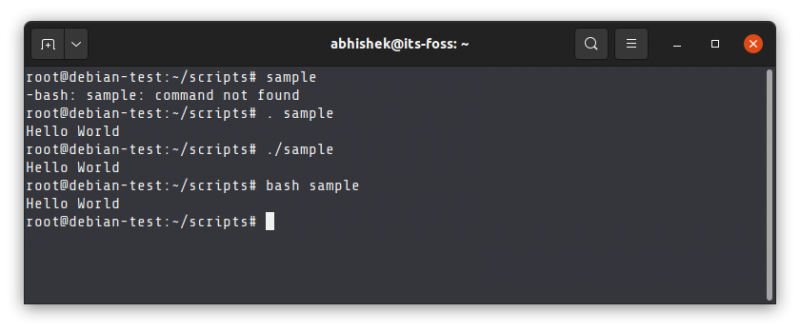
Even if you are in the same directory and try to run an executable script just by its name, it will show an error.
root@debian-test:~/scripts# sample
-bash: sample: command not foundYou need to either specify the shell interpreter explicitly or its absolute path.
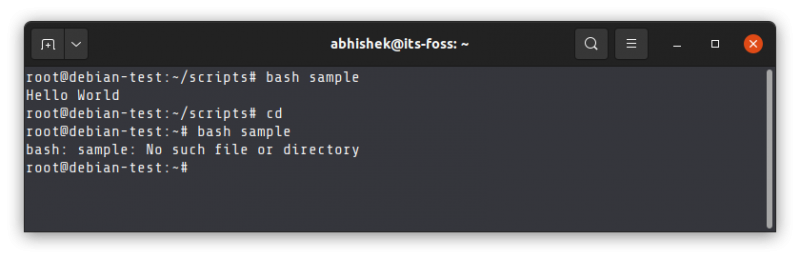
If you are in some other directory and try to execute the shell script without giving the correct path to the file, it will complain about not finding the file.
Adding it to the PATH
In some cases, you download the entire software in a tar file, extract it and find an executable file along with other program files. To run the program, you need to run the executable file.
But for that, you need to be in the same directory or specify the entire path to the executable file. This is tiresome.
Here, you can use the PATH variable. This variable has a collection of directories and these directories have the binary (executable) files of various Linux commands. When you run a command, your Linux system checks the mentioned directories in the PATH variable to look for the executable file of that command.
You can check the location of the binary of a command by using the which command:
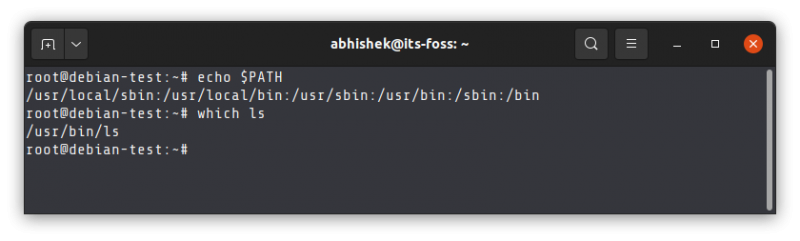
If you want to run an executable file or script from anywhere on the system, you need to add the location of the file to this PATH variable.
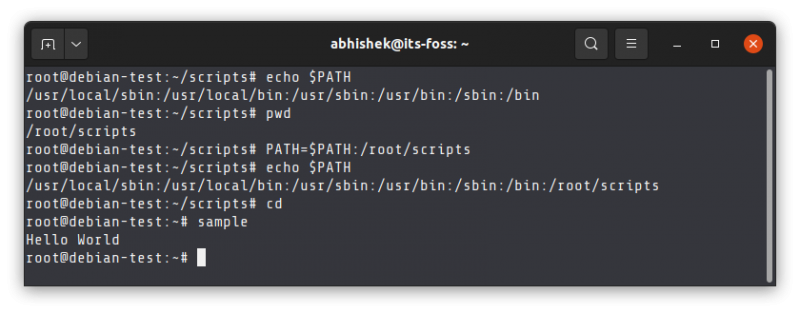
The PATH variable then needs to be added to the rc file of the shell so that the changes made to PATH variable are permanent.
You get the gist here. It is important that your Linux system has knowledge about the location of the executable script. Either you give the path while running it or you add its location to the PATH variable.
Did it help you?
I understand that when you are new to Linux, things could be overwhelming. But when you understand the root cause of the problem, it gradually improved your knowledge.
Here, there is no straightforward solution possible for the ‘command not found error’. I gave you some hints and pointers and that should help you in troubleshooting.
Similarly, you may encounter 'unable to locate package' error in Ubuntu. Here's what you need to know about it.

If you still have doubts or need help, please let me know in the comment section.
It's FOSS turns 13! 13 years of helping people use Linux ❤️
And we need your help to go on for 13 more years. Support us with a Plus membership and enjoy an ad-free reading experience and get a Linux eBook for free.
To celebrate 13 years of It's FOSS, we have a lifetime membership option with reduced pricing of just $76. This is valid until 25th June only.
If you ever wanted to appreciate our work with Plus membership but didn't like the recurring subscription, this is your chance 😃


